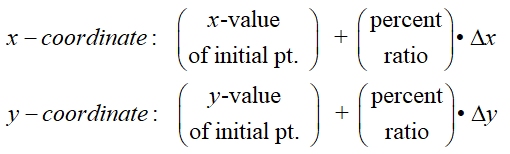Directed Line Segments - Partitions and Ratios MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Partition means to separate or to divide. A line segment can be partitioned into smaller segments which are compared as ratios.

We saw a partition of a line segment when we worked with the midpoint of a segment.
The midpoint divided (partitioned) the segment into two smaller segments
in a ratio of 1:1. Both smaller segments were equal in length.


The location of a segment's midpoint is the same distance when measured from either endpoint.

Unfortunately, this "same from both endpoints" idea, when applied to partitioning,
only works when the partition ratio is 1:1 (which is seldom the case).

For example, consider trying to find a partition point on the segment above
that is twice as far from dog as it is from cat (a ratio of 2:1).
A ratio of 2:1 starting at dog does not yield the same partition point
as a ratio of 2:1 starting at cat.

For this reason, we need to choose a starting point (the initial point) to
clarify where the partition point will be located on the line segment.
The solution will be true only from one endpoint of the segment (unless the ratio is 1:1).

Because of the need to establish a starting point to clarify the location of the partition point, partitions occur on line segments that are directed line segments. Remember, a directed line segment is a segment that has distance (length) and direction, with a "starting point" referred to as the "initial point", and a "terminal point". Let's take a quick review of the relationship between a partition ratio and a percent of whole ratio, as seen in Partitioning Line Segments. Partition Ratio 2:3 Notice: AP = 2 of the 5 equal parts, and PB = 3 of the 5 equal parts. 2/5 Percent of the Whole Ratio Notice that AP is 2/5 of the whole distance AB. Partition Ratio: (in fractional form)      compares AP to PB. (compares part : part) Percent of Whole Ratio: (in fractional form)         = compares AP to AB (the whole) (compares part : whole) Partitions and Ratios on Directed Line Segments: When working on a coordinates axes, there are several ways to find the coordinates of a "partition" point of a directed line segment (as we will see in the next lesson). This lesson will look at how to use our basic knowledge of similar triangles to arrive at coordinates of the partition point. Additional methods of solution will appear in the next lesson. Overview: We will be drawing right triangles, with the directed segment as the hypotenuse, and forming similar right triangles. We will use the fact that the corresponding sides of similar triangles are in proportion to obtain lengths to locate the partition point. 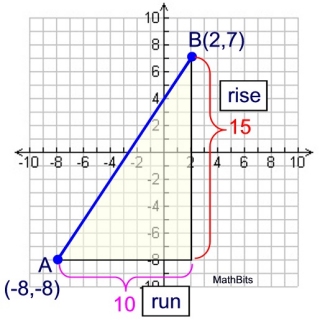Question: If P partitions a directed line segment starting at A(-8,-8) and ending at B(2,7) in a ratio of 2:3, find the coordinates of P. Solution: The partition ratio = 2:3 The percent of whole ratio = 2:5 Draw the yellow right triangle, as shown, counting the lengths for the legs. Point P lies somewhere along , so we can drop a perpendicular down to the base of the yellow triangle, creating two similar right Δs. Each triangle has a right angle and the sharing of angle A which will satisfy the AA Theorem to prove triangles similar. In this situation, AP (hypotenuse) is 2/5 of the whole distance from A to B (hypotenuse), telling us that the ratio of similitude between the two similar triangles will be 2/5. * note the "percent of whole ratio" at work   Let's apply that ratio of similitude of 2/5 to the legs of the triangle, since we know that the corresponding sides of similar Δs are in proportion. Base leg yellow Δ = 10 Base leg green Δ = (2/5) • 10 = 4 Vertical leg yellow Δ = 15 Vertical leg green Δ = (2/5) • 15 = 6 Use these distances to draw the green Δ which will have a vertex at P. Add these lengths to the coordinates of point A to get the coordinates of point P. To A(-8,-8) add x-value of 4 and y-value of 6. P(-8 + 4, -8 + 6) = P(-4,-2)       RUN associated with : (2/5)(10) = 4           RISE associate with : (2/5)(15) = 6

If we combine these steps, we can create a simple pattern
for finding the x and y coordinates of the partition point.

Just remember that the first number is the x (or y) coordinate of the initial point A(-8,-8).

If you forget the pattern, you can relie on your knowledge
of similar triangles to solve the problem.

Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts