|
The beauty of mathematics is that there is always "another way"
to solve a problem,
or arrive at a conclusion.
Our task: to find the coordinates of a partition point on a directed line segment.
|
 Partition: Similar Triangles Method: (preferred method) Partition: Similar Triangles Method: (preferred method)
In the last lesson, we saw how to use similar triangles to find the partition point.
We are listing that method as the "preferred method" because it utilizes past well-known skills, which will lead you to a solution even if you forget the pattern formula.

 Partition: Algebraic Formula Method
This method will use the concepts presented in the Similar Triangles Method to create an algebraic formula for the coordinates of the partition point. Partition: Algebraic Formula Method
This method will use the concepts presented in the Similar Triangles Method to create an algebraic formula for the coordinates of the partition point.
Remember that order is important. Start with the initial point, A. This starting point, A, will be labeled (x1,y1), and the terminal point, B, will be labeled (x2,y2).
The concepts from the Similar Triangles Method are being expressed as variables to produce this formula.
• Let the endpoints be A(x1, y1) and B(x2, y2).
• The "run" is the change in the x-coordinates:
(x2 - x1) or Δx
• The "rise" is the change in the y-coordinates:
(y2 - y1) or Δy
• For the partition ratio, let the numerator = a and the denominator = b, for a ratio of a/b.
• For the percent of whole ratio, use a/(a+b).
|
|
The coordinates of P can be found using this formula, which is presented in the form of an ordered pair of coordinates:

In words: The x-coordinate of P will be the x-coordinate of A + the percent of whole ratio times
the "run" of the line segment. The y-coordinate of P will be the y-coordinate of A + the percent of the whole ratio times the "rise" of the line segment.
Since (x2 - x1) and (y2 - y1) can be expressed as Δx and Δy, this formula can also be:
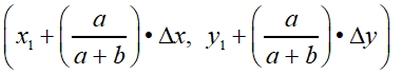
|
|
This is a more "algebraic" listing of the formula we developed in the last lesson working with similar triangles. While this is a great algebraic formula, it may be difficult to remember. Keep in mind that using similar triangles, as shown in Partitions and Ratios, may be a more reliable way to remember how to find partition coordinates.
|
|

 Partition: Using Dilations Method Partition: Using Dilations Method
Does the formula we just saw look vaguely familiar? Okay! It may not look familiar,
but it does have many of the components of another formula we have seen.
Since we have been dealing with similar triangles, the concept of dilations may come to mind.
Formula for a dilation, center not at the origin:

O = center of dilation at (a,b); k = scale factor
Regarding directed line segment  , we will be dilating the endpoint B using the endpoint A as the center of the dilation. Since our partition point lies ON the segment, we will be dealing with a dilation which is a reduction (0 < k < 1). , we will be dilating the endpoint B using the endpoint A as the center of the dilation. Since our partition point lies ON the segment, we will be dealing with a dilation which is a reduction (0 < k < 1).
The image of the dilation will be the partition point, P.
The variables a and b do not represent the same quantities in the two formulas we are examining, so if we tweak this dilation formula to correspond to our given information, we may see the resemblance between the formulas more clearly.
Remember, the point being dilated is B, and its image will be the partition point P.
The center of our dilation is point A at (x1, y1), so we will replace a with x1 and b with y1.
The point being dilated is B, so we will replace x with x2 and y with y2.

If we rearrange a couple of terms (commutative property), we will get:

Let's compare this improved dilation formula to our previous formula for finding P:

Notice: 
The scale factor of the dilation, k, is equal to the ratio of AP to the total length AB.
 If you choose to use this dilation method when partitioning segments, remember that the "partition ratio" (2/3 in this case) is NOT the scale factor. If you choose to use this dilation method when partitioning segments, remember that the "partition ratio" (2/3 in this case) is NOT the scale factor.
The "percent of whole ratio" representing the portion of the whole segment length AB
is the scale factor (2/5 in this case). |
|

 Partition: Side Splitter Theorem Method Partition: Side Splitter Theorem Method
The Side Splitter Theorem and the Partition Construction both work off the same principle.
| Side Splitter Theorem: If a line is parallel to a side of a triangle and intersects the other two sides, then this line divides those two sides proportionally.
 |

x = 3.5
|
A corollary to this theorem states that if three parallel lines intersect two transversals, then the segments intercepted on the transversals are proportional. |
Partition Construction:
The partitions from A to B are of equal measure because the blue dots along the diagonal line were marked off to be equal in measure and parallels were constructed. The Side Splitter Corollary ensures that the segments intercepted on the transversals are proportional (in this case 1:1).
|
Example: A directed line segment has an initial point at A(4,12) and a terminal point at B(19,2). Find the coordinates of the partition point P with a ratio of 2:3.
 |
1. We know that the "percent of whole ratio" will be 2:5 and that the whole segment will be divided into 5 equal pieces.
2. We can place P on the second dot from A, since the "partition ratio" is 2:3.
3. Using the Partition Construction, shown above, divide the given segment into 5 equal pieces. (The construction lines have been removed from the diagram. Only the finished segment remains.) |
4. Draw a right triangle showing the "rise" (Δy) and "run" (Δx) values for this line segment of -10 and 15, respectively.
We will now be using the Side Splitter Corollary (dealing with transversals and parallel lines).
5. From the given segment, drop (construct) perpendiculars from the red dots, to the horizontal base. Since these perpendicular lines are parallel, they will divide the horizontal leg of the triangle into equal pieces, since there are equal divisions on the given segment.
If 15 is divided into 5 equal parts, each part will equal 3 (and two of those parts = 6).
6. From the given segment, construct perpendiculars from the red dots, to the vertical leg of the triangle. The same reasoning used in step 5 is true.
If -10 is divided into 5 equal parts, each part will equal -2 (and two of those parts = -4).
7. Starting from point A, we have for the x-coordinate: 4 + 6 to the right = 10.
And for the y-coordinate we have 12 + -4 down = 8.
The coordinates of P are (10,8). |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|