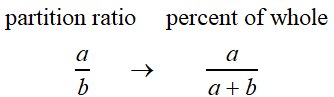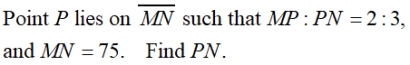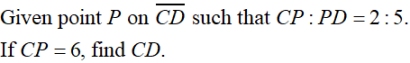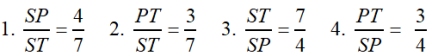Let's take a look at working with partitions and ratios in relation to line segments,
and set up the skills needed for dealing with directed line segments in the next lesson.
|
Partition means to separate or to divide. A line segment can be partitioned into smaller segments which are compared as ratios. |
|
Algebra 1 worked with problems dealing with partitions and ratios in line segments.
Example 1: Algebraic
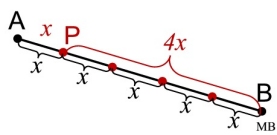
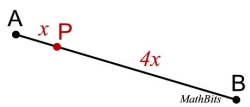
Given the line segment from point A to point B.
The length, AB, measures 35 inches.
If the ratio of AP to PB is 1 to 4, find AP and PB.
|
 |
That was easy! Now, let's take a closer look at what was happening in Example 1.
The "partition ratio" gives the relationship between the two parts of the segment.
The "percent of whole ratio" give the relationship between one part and the whole segment.
The percent of whole ratio can be found
by adding the numerator from the partition ratio to its denominator. |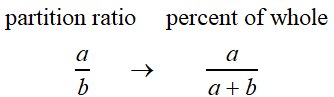
Let's summarize how the partition ratio and the percent of whole ratio are related:
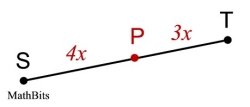
Partition Ratio 3:2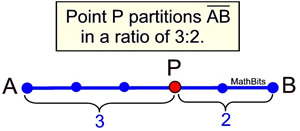
Notice: Always start from first letter in segment name unless told otherwise. |
Percent of the Whole Ratio 3/5
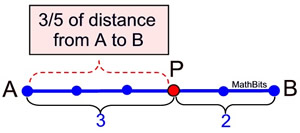
Ratio AP:PB = 3:2
means AP is 3/5 of AB. |
Summary:
•
Partitioning 
into a 3:2 ratio implies starting at point A.
• The ratio of 3:2 indicates that the segment will actually be divided into 5 equal sections.
• If P is the partition point, it will be located 3 of the 5 equal sections away from A and 2 of the 5 equal sections away from B. Point P is closer to point B.
• 3/5 is the percent of whole ratio, where AP is 3/5 of AB
Take a look at a few more examples, to be sure you clearly understand these ratios.
Example 2:
|
 |
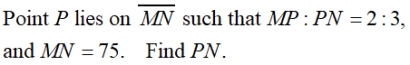
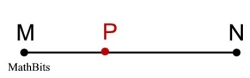Example 3:
|
 |
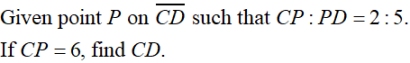
It is important to remember that given a "part : part ratio", like the partition ratio,
you can quickly state the "part : whole ratio", such as the percent of whole ratio.
is actually partitioned into 
