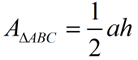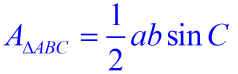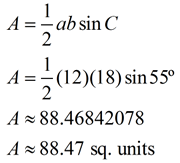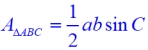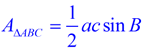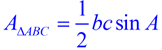Area of Triangle Using Trigonometry MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

A Trigonometric Formula for the Area of a Triangle:
The general formula for the area of a triangle is well known. While the formula shows the letters b and h, it is actually the "pattern" of the formula that is important. The area of a triangle equals ½ the length of one side times the height drawn to that side (or an extension of that side).	General Formula for Area of Triangle: b = length of a side (base) h = height draw to that side
The area of ΔABC can be expressed as: 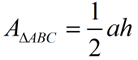where a represents the side (base) and h represents the height drawn to that side.

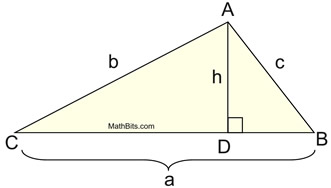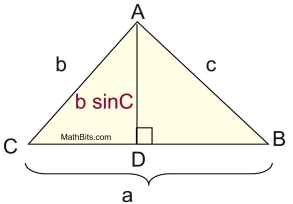
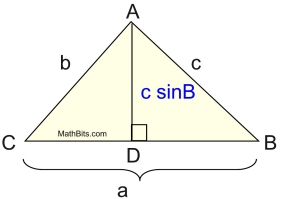
Using trigonometry, let's take another look at this diagram.
In the right triangle CDA, we can state that:

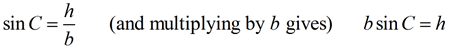
The height, h, of the triangle can be expressed as b sin C.

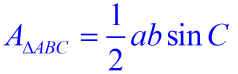
Substituting this new expression for the height, h, into the general formula for the area of a triangle gives: where a and b can be any two sides and C is the included angle.

The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. AreaΔ = ½ ab sin C. You may see this referred to as the SAS formula for the area of a triangle.

With this new formula, we no longer have to rely on finding the altitude (height) of a triangle in order to find its area. Now, if we know two sides and the included angle of a triangle, we can find the area of the triangle. This is a valuable new formula!

And again, it is the "pattern" of using two sides and the included angle that is important to remember. The area of a triangle equals ½ the product of two sides and the sine of the angle between these two sides.

Given the triangle at the right, find its area. Express the answer to the nearest hundredth of a square unit.
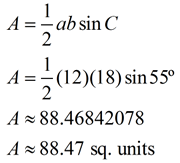When using your graphing calculator, be sure you are in DEGREE mode, or using the degree symbol.	Let a = ST, b = RT, and C = ∠RTS.

Given the parallelogram shown at the right, find its area to the nearest square unit. The diagonal of a parallelogram divides it into two congruent triangles. So the total area of the parallelogram will be TWICE the area of one of the triangles formed by the diagonal. This example shows that by doubling the triangle area formula, we have created a formula for finding the area of a parallelogram, given 2 adjacent sides (a and b) and the included angle, C. Area of Parallelogram

Let a = PS, b - RS, and C =∠PSR.

Given the parallelogram shown at the right, find its EXACT area. If a question asks for an EXACT answer, do not use your calculator to find the sin 60º since it will be a rounded value. To get an EXACT value for sin 60º, use the 30º-60º-90º special triangle which gives the sin 60º to be . Notice that we are using the formula for the area of a parallelogram we discovered in Example 2.

Let a = AD, b = AB, and C = ∠BAD.

For help with this formula on your calculator, click here.

Derive (or Justify) this formula:
NOTE: The NY Next Generation Standards ask for students to "justify" this formula for finding the area of any triangle. This is accomplished by drawing an auxiliary line from a vertex perpendicular to the opposite site. While this last statement may be interpreted as applying only to acute triangles, the wording of "any triangle" in the previous sentence may imply including obtuse triangles (but is unlikely). This site will examine both "acute" and "obtuse" triangles in relation to this formula.

Case 1: Acute Triangle

At the top of this page, we saw how the new formula was developed
by expressing the height, h, as bsinC. Remember, AD = h.

If this formula truly works (and it does!), we should be able to apply the formula using any angle in the triangle. So, when attempting to "justify" this formula, we should show that it can be "developed" using any (and every) angle in the triangle. • Using acute ∠C, we have sin C = h/b, which gives h = bsin C, giving the formula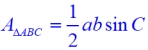
• Now, using acute ∠B, we have sin B = h/c, which gives h = csin B, giving another version of the the formula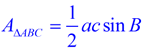
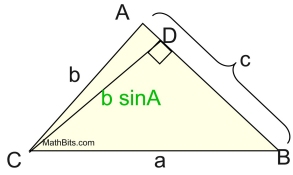
• Finally, using acute ∠A, with a new height value, h = CD, we have sin A = h/b, which gives h = cbsin A, or h = bcsinA. ,, giving the third version of the the formula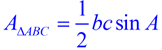

 

Case 2: Obtuse Triangle
Can we still develop this formula if ∠A is an obtuse angle?

The answer is "yes", but it will require more work and some more trigonometric information. We will take a brief look at what is involved when ∠A is an obtuse angle, but these concepts will be more fully developed in upcoming courses.

Note: to maintain the use of a single letter to represent the angle in our formula, we will be referring to ∠BAC in the diagram below, as simply∠A. No, this is not normal, but it will make reading the problem easier.

Will we be justifying the formula: 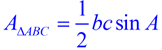When ∠A is an obtuse angle, the altitude drawn from C or B will be outside of the triangle. Draw the altitude from C to the line containing the opposite side. ΔCAE is a right triangle, but unfortunately it does not contain ∠A that we need for our formula.
We know, however, that ∠CAE is supplementary to ∠A, since they form a linear pair. We can state that m∠CAE = 180 - m∠A and from ΔCAE that 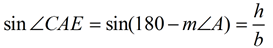. If we apply a trigonometric fact that sin∠A = sin(180 - m∠A), we can substitute and get: (After multiplying both sides of the first equation by b.) Now, substitution into the general formula for the area of a triangle will give us our desired formula: .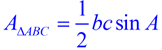

sin∠A = sin (180 - m∠A) Remember that the functions of sine, cosine, and tangent are defined only for acute angles in a right triangle. So, how do we find the sine of an obtuse angle? We cannot use the sides of the triangle to find sin∠BAC because the angle does not reside in a right triangle. We can, however, find sin∠BAD which deals with an acute angle in a right triangle. ∠BAD is the supplement of ∠BAC since they form a linear pair. The sine of an obtuse angle is defined to be the sine of the supplement of the angle. Thus, sin∠A = sin (180 - m∠A). On your graphing calculator, sin(50º) = 0.7660444431 and sin(130º) = 0.7660444431show this fact to be true. These angles are supplementary since 50º + 130º = 180º.

WHY does sin∠A = sin (180 - m∠A)? This topic will be explored in more detail in upcoming courses. To understand "why" this relationship is true, we need a coordinate grid. Right triangle DEF is drawn in quadrant I, as shown. If we draw an angle of 130º, and drop a perpendicular to the x-axis from point H where DH = DF, we will create a reflection of ΔDEF over the y-axis. This reflected triangle (ΔDGH) is congruent to ΔDEF and both triangles have the same lengths for their sides opposite the 50º. It should be noted that both opposite sides deal with positive y-values (designating direction above the x-axis).

50º and 130º are supplementary.

When dealing with obtuse angles (such as 130º), the corresponding acute angle (50º) is used to determine the sine, cosine or tangent of that obtuse angle. This corresponding acute angle is called a "reference angle".