|
NOTE: The strategies for proofs of the theorems stated on this page are presented in " descriptive paragraphs".
In some cases, "formal" proofs may require expanding on these details.
|
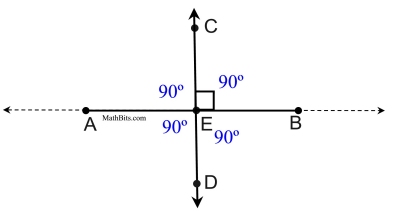
Two lines in the same plane are perpendicular if and only if they form a right angle. |
|
Perpendicular lines (or segments) actually form four right angles, even if only one of the right angles is marked with a box.
The statement above is actually a theorem which is discussed further down on this page. |
 |
You may also see this definition stated as:
"If two lines intersect and form adjacent angles of equal measure, the lines are perpendicular." |
There are a couple of provable concepts relating to perpendicular lines that are intuitively just common sense:
1.  The shortest distance from a point to a line is the perpendicular distance.
Proof:
Draw perpendicular from P to C with m∠C = 90º. Draw ΔPCA with A on m. m∠P+m∠C+m∠A=180.
m∠P+m∠A=90, making ∠A an acute angle and
m∠A < m∠C
. PC < PA (In a Δ, shorter side opp. smaller angle.). Since A can be located anywhere on line m, PC will be the shortest length.
Intuitively: Any distance, other than the perpendicular distance, will be the hypotenuse of the right triangle, making it longer than PC.
|
.
|
2. In a plane, through a point not on a line, there is one, and only one, perpendicular to the line.
Indirect Proof:
If we assume there are two perpendiculars to line m from point P, we will create a triangle containing two right angles. The measure of ∠P will be 0º (since the sum of the angle measures in a Δ = 180º) forcing both perpendiculars to coincide (be the same). Our assumption of 2 perpendiculars from P is not possible. |
 |
Perpendicular lines can also be connected to the concept of parallel lines:
3. In a plane, if two lines are perpendicular to the same line, the two lines are parallel.
If t ⊥ m and s ⊥ m, then t | | s.
Indirect Proof:
• There are only two possibilities: t | | s or t is not | | to s.
In a plane, two straight lines are parallel or they intersect.
• Assume t is not || s. Since the lines are not parallel, they must intersect at one point, call it P. Two straight lines can intersect in only one point. This is an assumption leading to a contradiction.
• Since it is given that t ⊥
m and s ⊥ m, we now have two lines through P that are perpendicular to m. BUT, in a plane, through a point not on a line, there is one, and only one, perpendicular to the line.
• The assumption leads to a contradiction.
• Therefore: t | | s
|
Indirect Proof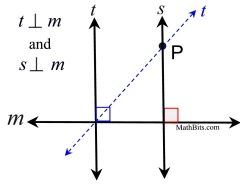
|
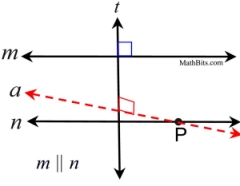
4. In a plane, if a line is perpendicular to one of two parallel lines, it is also perpendicular to the other line.
If m | | n and t ⊥ m, then t ⊥ n.
Indirect Proof:
• Assume t is not ⊥ n. This is an assumption leading to a contradiction.
• There can exist another line, call it a, that can be perpendicular to t that also passes through line n, say at P. So, t⊥a. Through a point not on a given line, this is only one perpendicular that can be drawn to the given line.
• Since t⊥ m and t⊥ a, then a || m. If two lines are perpendicular to the same line, the two lines are parallel.
• We were given that m | | n, and we now have a | | m. The problem is that line a and line n both pass through point P and are parallel to m. This contradicts the Parallel Postulate that says through a point not on line m, only one line can be drawn parallel to line m.
• The assumption leads to a contradiction.
• t ⊥ n
|
Indirect Proof
|
|
If two lines are perpendicular, they form four right angles. |
|
 |
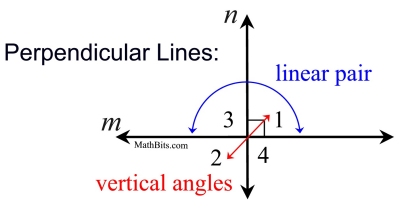It makes no difference "where" you label the "box", since all of the angles are right angles.
We will start with ∠1.
Proof:
Perpendicular lines form right angles so ∠1 is a right ∠ with a measure of 90º. Since vertical angles are congruent, ∠2 will be 90º and be a right angle.
∠1 and ∠3 form a linear pair and supplements. m∠3+m∠1=180. By subtraction, m∠3=90º making it a right angle. Vertical angles makes ∠4 same measure as ∠3 which is 90º, a right angle. |
|
If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular. |
|
Proof:
When two adjacent angles form a linear pair, their non-shared sides form a straight line (m). This tells us that the measures of the two angles will add to 180º. m∠1+m∠2=180. If these two angles also happen to be congruent (of equal measure), we have two angles of the same size adding to 180º. 2m∠1=180. So m∠1=90.
Each angle will be right angles making m ⊥ n.
|
|
|
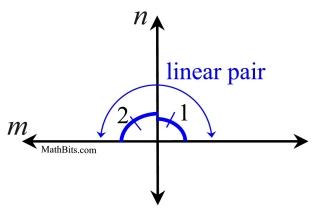
If two sides of two adjacent acute angles are perpendicular, then the angels are complementary. |
|
 |
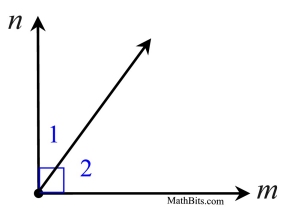Proof:
In the diagram at the left, ∠1 and ∠2 are acute adjacent angles whose non-shared sides are perpendicular, m ⊥ n.
Since perpendiculars form right angles (90º), we know the m∠1 + m∠2 = 90º, making the angles complementary, by definition. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
