 |
Remember -- use your compass
and straightedge only! |
|
Bisect a line segment
Note: This construction is also the construction for Perpendicular Bisector of a Segment.
|
|
Given:  (a line segment) (a line segment)
Construction: bisect  . .
Remember that "bisect" means to form two congruent segments.
|
 |
This construction will also establish that the bisector is perpendicular to the given line segment.
STEPS:
1. Place your compass point on A and stretch the compass MORE THAN half way to point B (you may also stretch to point B).
2. With this length, swing a large arc that will go above and below  . .
3. Without changing the span on the compass, place the compass point on B and swing the arc again. The two arcs need to be extended sufficiently so they will intersect in two locations (one above the segment and one below the segment).
4. Using your straightedge, connect the two points of intersection with a line or segment to locate point C which bisects the segment.
 |
You may also see this construction done where only small portions of the arcs are shown both above and below the segment. The larger arcs, as shown here, are often easier to remember (since they form a "crayfish" looking creature) and they visually reinforce the circle concept needed for the proof of this construction. |
 See Contruct: Divide a Segment to see what happens when you bisect a segment, See Contruct: Divide a Segment to see what happens when you bisect a segment,
then bisect the parts, and continue this bisecting process.

Proof of Construction: Label the points of intersection of the arcs with the letters D and E. Draw segments  These four segments will be congruent as they are the radii of two congruent circles. We now know that point D is equidistant from points A and B. And we know that point E are also equidistant from points A and B. Theorem: "The points on a perpendicular bisector of a line segment are equidistant from the endpoints of the line segment." Therefore, These four segments will be congruent as they are the radii of two congruent circles. We now know that point D is equidistant from points A and B. And we know that point E are also equidistant from points A and B. Theorem: "The points on a perpendicular bisector of a line segment are equidistant from the endpoints of the line segment." Therefore, 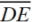 is the perpendicular bisector of is the perpendicular bisector of 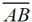 . (And . (And 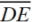 bisects bisects 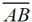 .) .)
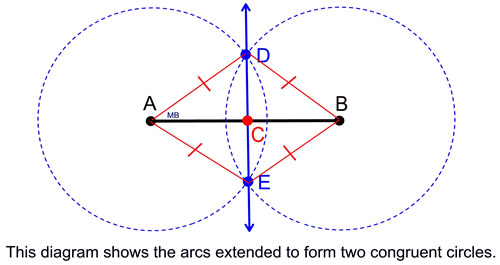

Alternative Proof Using Congruent Triangles:
 |
The congruent triangle proof of this simple construction is quite lengthy.
Here we go! |
|
Proof of Construction: Label the points of intersection of the arcs with the letters D and E. Draw segments  These four segments will be congruent as they are the radii of two congruent circles. We can now show that there are four congruent triangles in this diagram giving us the congruent segments that will prove that the bisecting has occurred. This proof will use two sets of congruent triangles. These four segments will be congruent as they are the radii of two congruent circles. We can now show that there are four congruent triangles in this diagram giving us the congruent segments that will prove that the bisecting has occurred. This proof will use two sets of congruent triangles.

|
Now, ∠BDE  ∠ADE since corresponding parts of ∠ADE since corresponding parts of  Δs are Δs are  (CPCTC). (CPCTC).
|
|
Perpendicular:
We also have
∠DCA  ∠DCB by CPCTC. ∠DCB by CPCTC.
These ∠s form a linear pair making them supplementary.
m∠DCA + m∠DCB = 180 (definition of supplementary).
By substitution, m∠DCA +
m∠DCB = 180, making
m∠DCA = 90.
∠DCA is a right angle by definition, making  since ⊥lines form rt.∠s. since ⊥lines form rt.∠s.
|
 |
Notice that after this construction, the 4 sides of quadrilateral ADBE are congruent making ADBE a rhombus. We know that the diagonals of a rhombus bisect each other and are also perpendicular, supporting our construction. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|






