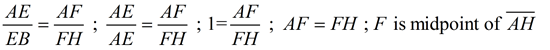We will start our investigation of the
classical triangle centers with the
centroid.
|
A point of concurrency is the point where three or more lines intersect. |
|
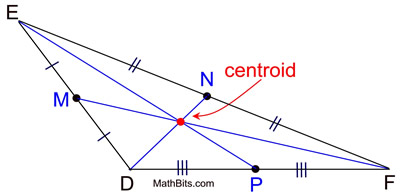
This discussion will focus on the name given to the point where the medians of a triangle
in a construction intersect. That point is called the centroid.
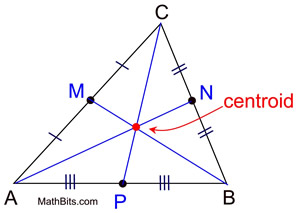
The median of a triangle is a segment joining any vertex to the midpoint of the opposite side.
The term "centroid" is Greek implying the center of the triangle,
and can be used as a substitute for "center of gravity" or "center of mass"
.

 Centroid - concurrent medians
Centroid - concurrent medians
"centroid" - Greek "centre" meaning center
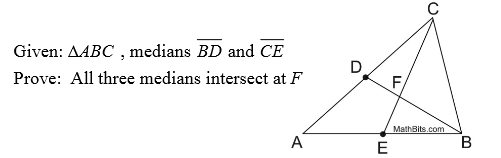
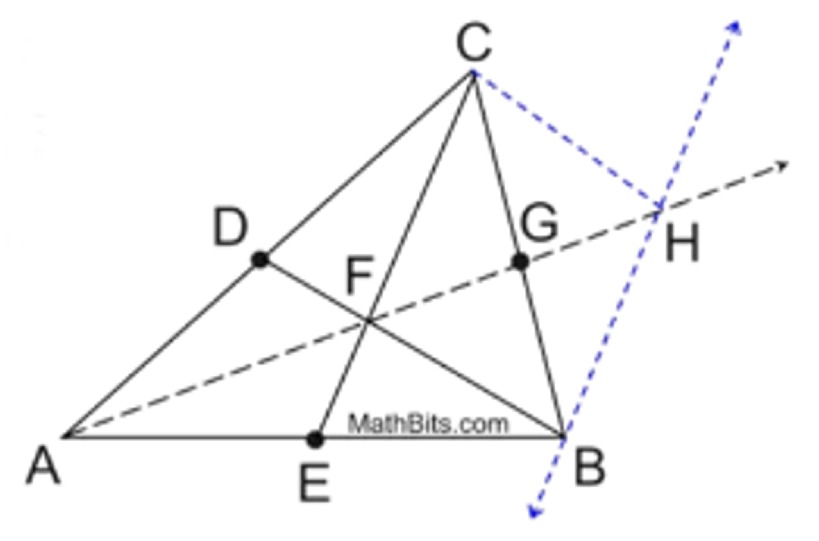
The three medians of a triangle are concurrent, meaning they intersect in one common point.
The point of concurrency of the medians is called the centroid of the triangle.
Unlike the "incenter" and the "circumcenter", the centroid is not connected to a circle in relation to the triangle (such as is seen with the inscribed circle and the circumscribed circle).

The medians of a triangle are
always concurrent in the interior of the triangle.
Let's take a look at the locations of the centroid in a couple of different triangles.

The centroid divides the medians into a 2:1 ratio.
The portion of the median nearest the vertex is twice as long as the portion connected to the midpoint of the triangle's side. For example, in ΔABC, shown above, if the length from C to the centroid is 10 units, then the distance from the centroid to P is 5 units.

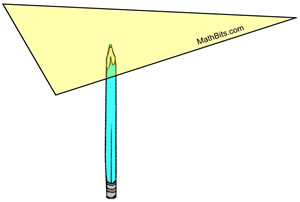
Archimedes showed that the point where the medians are concurrent (the centroid) is the center of gravity of a triangular shape of uniform thickness and density.
If you cut a triangle out of cardboard and balance it on a pointed object, such as a pencil, the pencil will mark the location of the triangle's centroid (center of gravity or balance point). |
|

Construction of a centroid:
We have seen how to construct a median of a triangle. Simply construct the three medians of the triangle. The point where the medians intersect is the centroid.
 Be sure to find the intersection of the medians (the red dot) and NOT the intersection of the segment bisectors used to locate the midpoints (the black dot). Be sure to find the intersection of the medians (the red dot) and NOT the intersection of the segment bisectors used to locate the midpoints (the black dot).
|
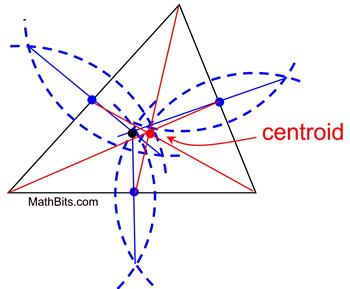 |
Actually, finding the intersection of only 2 medians will find the centroid. Finding the third median, however, will ensure more accuracy of the find. |

FYI:
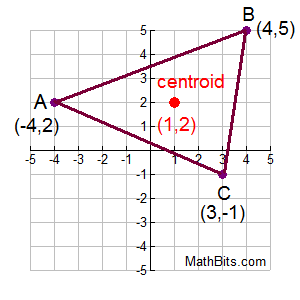
When working in the coordinate plane, the coordinates of the centroid of a triangle can be found by taking the average of the x coordinates of the three vertices, and the average of the y coordinates of the three vertices.
Add the x-coordinates and divide by 3.
Add the y-coordinates and divide by 3.
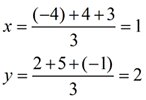 Centroid (1,2) |
|



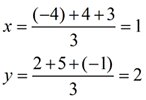 Centroid (1,2)
Centroid (1,2)