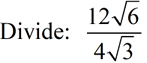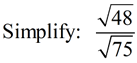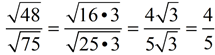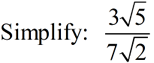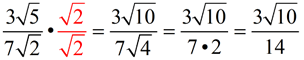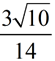In Algebra 2, we will be encountering problems that require the arithmetic and simplifying of square roots and roots of a higher index. Let's start by reviewing what we already know about working with square roots, from previous courses.
Simplifying Square Roots: |
Remember: To "simplify a radical" does not mean to estimate the radical in decimal form.
To "simplify a radical" means to express the radical in another "form"
which is equivalent to the given radical.
This new "form" will most likely contain another radical.
 |
A square root is in simplest form when
1.
the radicand contains no perfect square factors
2. the radicand is not a fraction
3. there are no radicals in the denominator of a fraction. |
|
 
• Find the largest perfect square factor (the largest perfect square that divides into 48 with no remainder). You need to be familiar with a list of perfect squares.
• Give each factor its own radical sign. 
• Reduce the "perfect square" radical that was created.
• ANSWER: 
 
The number out front is being multiplied times the radical, and will carry through the problem.
 
Separate the problem by giving the numerator and denominator their own radical symbols.
While this solution may be better, it is still not in simplest form, since it leaves a radical in the denominator. You now need to "rationalize the denominator". This simply means that we want the denominator to be a "nice" rational number, not a radical. An "integer" would be nice.
We need to get that number under the radical to be a perfect square, to remove the radical symbol.
Create a perfect square in the radicand of the bottom radical by multiplying the entire problem by a fraction that will create a perfect square and whose fractional value is "one".
 
Some radicals cannot be simplified. The number 23 cannot be factored by any of the perfect squares (23 is prime). This is a trick question as it is already in simplest form and cannot be reduced further.
Arithmetic of Square Roots: |
 You can add square roots when they have the same index and same radicand (number under the radical). Just add the numbers in front of the radicals.You can think of it as "combining like terms".
To multiply square roots, multiply under the radicals and multiply any value in front of the radicals. Simplify answer if possible.
 
Multiply in the same manner as you would multiply two algebraic binomial terms. Distribute across the parentheses (FOIL).
 |
ANS:  |
To divide square roots, divide the values outside the radicals and divide the values inside the radicals. Simplify if needed.
To "simplify", requires a rationalized denominator. Remember to multiply the denominator to create a perfect square as the radicand, if you are dealing with a radical in the denominator.
Working with radicals on the graphing calculator:
|
For
calculator help with entering
radicals.
click here. |
|
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
