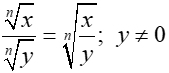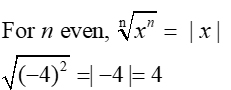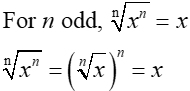|
The following properties (rules) are used when working with radicals of all indices.
Let x and y be real numbers, variables, or algebraic expressions that yield real numbers,
and let m and n be positive integers.
Radicals and powers are inverse operations.
Taking the square root will undo the process of squaring.
Taking the cube root will undo the process of cubing.
 Properties of Radicals (Rules):
| Property (Rule): |
Symbolism: |
In plain English ... |
Root to the Root Power
(Inverse) |
 |
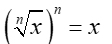An n-root radical raised to the n-power returns the radicand (the inside). The inverse at work. |
| Product Rule |
|
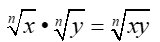
When multiplying, and the roots, n, are the same, keep root, multtply inside. |
| Quotient Rule |
 |
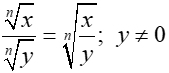When dividing, and the roots are the same, keep the index and divide the values inside. |
| Radical to a Power |
 |
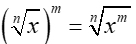When raising a radical to a power, keep the index, and raise the inside to the power. |
| Root of a Root |
 |
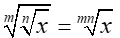When taking the root of a root, multiply the indices, and keep the radicantd. |
| Even Root Rule |
 |
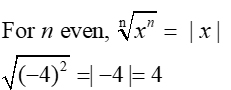For even roots, the root raised to the same power = absolute value of the inside. This keeps only 1 positive root as the solution (principal root).. |
| Odd Root Rule |
 |
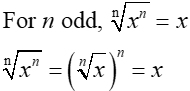For odd roots, the root raised to the same power gives the inside radicand.
It is the inverse property at work. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
