Remember the primary rule for working with linear inequalities:
... multiplying or dividing by a negative number
changes the direction of the inequality. |
|
A compound inequality is two simple inequalities joined by the word "and" or "or".
(It is also possible that a compound inequality may contain an inequality and an equation.)
Examples: x < 5 and x > -2 a + 2 > 4 or a + 3 = 6
Note: Statements such as x < 5 and x >-2, that have a common element ("x" in this case),
may be written in a "sandwich" format as -2 < x < 5.
These two different forms of the statement are equivalent.
 Using the word " and ":
(where both inequalities are true)
|
| • A solution to the compound inequality is a solution to both inequalities. |
• "AND" - both must be true |
• The compound inequality graph is the intersection of the graphs of the two inequalities. |
• "Intersection" is where the separate answers overlap. |
• NOTATION:
can be written as:
or as:
[3x + 2 < 5]∩ [x + 2 > -4]
|
|
Using the word " or ":
(where one, or both, inequalities are true) |
• A solution to the compound inequality is a solution to at least one of the inequalities. |
• "OR" - either one, or both, must be true |
• The compound inequality graph is the union (joining together) of the graphs of the two inequalities. |
• "Union" is the combination of all the answers.
|
• NOTATION:
can be written as:
or as:
[3x + 2 < 5]∪[x + 2 > -4] |
|
• QUICK SAMPLE:
Find values that satisfy:
3x - 9 < 12 and 3x - 9 > -3
Sandwich the common statement (3x - 9) between the two inequalities
. -3 < 3x - 9 < 12
6
< 3x < 21
2 < x < 7
The solution is 2 < x < 7,
which can be read x > 2 and x < 7.
Interval notation: [2, 7]
|
|
• QUICK SAMPLE:
Find values that satisfy:
2x + 3 < 7 or 5x + 5 > 25
Solve first inequality
2x + 3 < 7
2x < 4
x < 2 |
Solve second inequality
5x + 5 > 25
5x + 20
x > 4 |
The solution is x < 2 or x > 4.
Interval notation: 
|
|
Solving Compound Linear Inequalities: |
|
For calculator help with compound linear inequalities
click here. |
|
|
Graph the solution set of: -3 < x < 4 |
This problem deals with TWO inequalities at the same time:
( -3 < x AND x < 4).
The solution set for this problem will be all values that satisfy both -3 < x AND x < 4, at the same time.
|
|
Look for where the two inequalities overlap (see the red graphings shown above).
Graph using open circles for -3 and 4 (since x can not equal -3 nor 4), and a bar to show the overlapping section.
|
Graph the solution set of: x < -3 or x 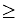 1 |
Again, this problem is dealing with two inequalities at the same time. But this time, the two inequalities do not overlap one another.
Notice that there is one open circle (for -3) but one closed circle (for 1). |
The solutions can lie in either section
of the plotted graphs shown above. |
Solve and graph the solution set of: |
Solve each inequality separately.
Combine the solutions.
Since this problem is "and", graph where the solutions intersect with one another.
Note: The solution x < 1 and x > -6 can also be written as -6 < x < 1.
The graph will be the overlapping of the two separate graphs. Graph using an open circle for both -6 and 1 (x can not equal -6 nor 1) since our symbols are simply less than or greater than.
|
x < 1 and x > -6  Other notations:
|
Solve and graph the solution set of: 5 + x > 7 or x - 3 < 5 |
Solve each inequality separately.
Combine the solutions.
Since this problem is "or", graph where both solutions are true.
Graphing where both solutions are true covers the entire number line. Any number on the number line will make "one" or "both" of the inequality true.
|
Other notations:
 |
Solve and graph the solution set of: x < 4 and x ≠ 1 |
Since this problem is "and", graph where the two inequalities intersect -- where BOTH are true.
|
x < 4 and x ≠ 1
Other notations:
 |
Solve and graph the solution set of: 2x - 1 < 5 and 2x - 1 > -2 |
Solve each inequality separately.
Combine the solutions.
Since this problem is "and", graph where the solutions intersect with one another.
Note: This problem can also be written as -2 < 2x - 1 < 5. When solving for x in this form, be sure to perform any changes to all three components of the inequality.
|
• Add 1 to all three sections.
• Divide all three sections by 2. |
|
Other notations:
 |
Applied Problem Using "AND" |
| The antifreeze added to your car's cooling system claims that it will protect your car to -35º C and 120º C. The coolant will remain in a liquid state as long as the temperature, in Celsius, satisfies the inequality -35º < C < 120º. Write this inequality in degrees Fahrenheit. |
Solution:
Remember: 
Plan:
• set up inequality
• substitute for C
• solve for (isolate) F |
 |
|
|
Answer: The coolant will remain in a liquid state as long as the temperature in Fahrenheit degrees satisfies the inequality
-31º < F < 248º |
Applied Problem Using "OR" |
The height of a horse is measured in a vertical line from the ground to the withers (at the base of the neck). Horses are measured in "hands" where one hand = 4 inches. If a horse is more than an exact number of hands high (hh), the extra inches are given after a decimal point, e.g. 14 hands 2 inches is written as 14.2 hh. Normal riding horses are between 14.3 hh and 17 hh, inclusive. Horses shorter than 14.3 hands are called ponies and horses over 17 hh are often called draft (or work) horses.
|
a.) Write an inequality statement to represent the heights, h, of normal riding horses in inches.
b.) Write an inequality statement stating the heights, in inches, of equines (horses) that do not fit the normal riding horse height specifications.
|
|
Solution:
a.) Normal riding horse heights in hands:
14.3 hh < h < 17 hh
Answer: Normal riding horse height in inches:
59" < h < 68"
|
Convert to inches.
14.3 hh = 14(4) + 3 inches
= 59 inches
17 hh = 17(4) inches
= 68 inches |
|
b.) Equines outside of the normal riding
horse heights in hands:
h < 14.3 hh or h > 17 hh |
Use conversions from part a. |
Answer: Equine heights in inches not fitting the normal riding horse heights:
h < 59" or h > 68" |
|
|
