You have already worked with inequality statements.
Let's refresh those skills and toss in a few new items and terms.
 |
The purpose of inequalities is to compare two values (or expressions). |

| Notations for Inequalities: |
| Inequality Notations: |
a > b ; a is strictly greater than b |
a 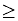 b ; a is greater than or equal to b |
a < b ; a is strictly less than b |
a 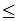 b ; a is less than or equal to b |
a ≠ b ; a is not equal to b |
Hint: The "open" (wider spread) part of the inequality symbol always faces the larger quantity. |
Notations without the "or equal to" portion of the symbol (such as just > or just < )
are referred to as Strictly Increasing, or Strictly Decreasing.
The term "strictly" does not allow for "equal to".
The expressions with equality included ( < or > ) are referred to as just Increasing or Decreasing.
Forms of notation include:
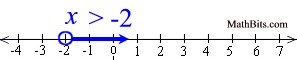
1. Inequality Symbol: x > -2
2.
Text: x is greater than negative two
3. Set-Builder Notation: 
4. Interval Notation: (-2, ∞)
|
Displayed on Number Line:
|
(see more about forms of notations at Notations for Solutions)

| Basic Properties of Inequalities: |
(properties apply to  )
)
If a > b, then a + c > b + c. |
Addition Property of Inequality |
If a > b, then a - c > b - c. |
Subtraction Property of Inequality |
If a > b and c > 0, then ac > bc. |
Multiplication Property of Inequality
|
Notice that c > 0.
If c < 0, reverse the direction of the final inequality. |
If a > b and c > 0, then  . |
Division Property of Inequality |
| If a < b and b < c, then a < c. |
Transitive Property of Inequality |
| If a > b then b < a. |
Sometimes called the "Reversal Property". (Converse) |
We saw in the Real Number Chart a property called the Law of Trichotomy.

 This Law of Trichotomy describes the only three relationships
This Law of Trichotomy describes the only three relationships
that can exist between two values. ("tri" measn three).
a > b, a = b, a < b
In essence, this law states that every real number is either positive, negative or zero.
(Consider b = 0 to see why this statement is true: a > 0, a = 0, a < 0.)

| Verify Rule for Solving Inequalities: |
|
 Remember: |
The process of solving a linear inequality is the same as solving a linear equation, except ...
... when you multiply (or divide) an inequality by a negative value,
you must change the direction of the inequality. |
 Let's first get an intuitive idea of what is happening
Let's first get an intuitive idea of what is happening
and why this "exception" is actually needed.
We know that 3 is less than 7.
Now, lets
multiply both sides by -1.
Examine the results (the products). |
... written 3 < 7.
... written (-1)(3) ? (-1)(7)
... written -3 ? -7
|
On a number line, -3 is to the right of -7, making -3 greater than -7.
 -3 > -7
-3 > -7
We have to reverse the direction of the inequality,
when we multiply by a negative value, in order to maintain a "true" statement. |
 Now, let's look at a more algebraic justification
Now, let's look at a more algebraic justification
as to why this "exception" is actually needed.
Statement: If you multiply (or divide) both sides of an inequality by a negative value,
you will need to change the direction of the inequality.
1. If a > b, then -a < -b. |
1. Translation of statement (mult. by -1). |
2. a > b |
2. Start with the "given" a > b. |
3. a - b > b - b |
3. Subtract b from both sides. |
4. a - b > 0 |
4. Additive Inverse Property b - b = 0 |
5. a - a - b > 0 - a |
5. Subtract a from both sides. |
6. 0 - b > -a |
6. Additive Inverse, Additive Identity |
7. -b > -a |
7. Additive Identity Property |
8. -a < -b |
8. Read in reverse (converse) |