|
For all real numbers x, (not zero),
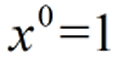
|
Any nonzero real number
with an exponent of 0
equals 1.
30 = 1
a0= 1
|

|
Let's see how, if we start with 1, we can end up with an exponent of zero:
For x ≠ 0: 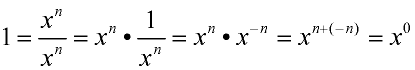
If we tried this argument for x = 0, we would be dividing by 0, which is not possible.

Examples: (numerical and algebraic applications)
1. 40 = 1
|
2. (-5)0 = 1
|
3. -20 = -1
Sneaky one!!!! Remember the exponent only affects the 2. If it affected the negative sign it would be written (-2)0.
|
4. 00 = undefined*
|
| * It seems to make sense that 00 should follow this rule and equal "one". But when you consider that 0 to any exponent (other than zero) is zero, could it be that 00 is zero? If this is not confusing enough, there are also cases where 00 yields an undefined result. For this reason, 00 is often called an indeterminate form. There is no unique universal answer as to the value of 00. |
5. xy0 = x•1 = x
x and y are real numbers, not zeros
|
6. 2(ab)0 = 2(1) = 2
a and b are real numbers, not zeros |
|