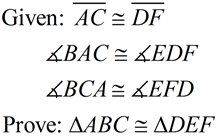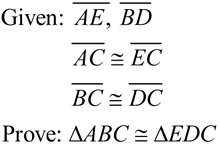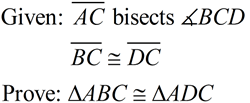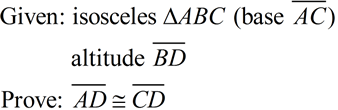|
When triangles are congruent, all pairs of corresponding sides are congruent, and all pairs of corresponding angles are congruent. Fortunately, it is not necessary to show all six of these facts to prove triangle congruence. We have seen the five ordered combinations of these six facts that can be used to prove triangles congruent. Now, let's look at some tips for working with congruent triangles.
 |
There are five ordered combinations to prove triangles congruent:
SSS, SAS, ASA, AAS, and HL (for right triangles). |
|
Tips for Preparing Congruent Triangle Proofs:
When working with congruent triangles, remember to:
1. |
Start by marking the given information on your diagram (using hash marks, arcs, etc.). |
2. |
Remember your definitions! If the given information contains "geometric words" such as midpoint, bisector, etc, be sure to use the definitions as they are "hints" to the solution. |
3. |
Look for any parts that your triangles may "share". These common parts may be one set of congruent parts. |
4. |
If you are missing needed pieces to prove the triangles congruent, examine the diagram to see what else you may already know about the figure. |
5. |
If you are trying to prove specific "parts" of the triangles (or other figures) are congruent, find a set of triangles that contains these parts and prove those triangles congruent first. |
6. |
If the triangles you need are overlapping, try drawing the two triangles separately. It may give you a better look at the known information. |
7. |
Keep in mind that there may be more than one way to solve the problem. |
A proof is like a big "puzzle" waiting to be solved.
Look carefully at the "puzzle" and use all of your geometrical strategies to arrive at a solution. |
Some of the more common (and popular) theorems and definitions used with congruent triangles:
|
 |
1. |
Angle Bisector - a ray in the interior of an angle creating two congruent angles. |
2. |
Segment Bisector - a line, segment or ray that divides the segment into two congruent parts. |
3. |
Midpoint of Segment - a point on the segment creating two congruent segments. |
4. |
Median of a Triangle - a segment from any vertex of a Δ to the midpoint of the opposite side. |
5. |
Altitude of a Triangle - a segment from any vertex of a Δ perpendicular to the line containing the opposite side. |
6. |
Vertical angles are congruent. These are the angles in the corners of an X. |
7. |
Right angles are congruent. Of course they are since they are all 90º. |
8. |
If two angles form a linear pair, they are supplementary. |
9. |
Points that lie on a perpendicular bisector of a segment are equidistant from the ends of the segment. |
| 10. |
If two parallel lines are cut by a transversal, the alternate interior angles are congruent. |
Of course, there are more theorems and definitions that may be used. |
Some of the more common properties and postulates
used with congruent triangles:
1. |
Reflexive Property - a quantity is equal (or congruent) to itself. Used for shared parts. |
2. |
Transitive Property - if two quantities are = to the same quantity, they are = to each other. |
3. |
Addition Property of Equality - when equals are added to equals, the sums are equal. |
4. |
Subtraction Property of Equality - when equals are subtracted from equals, results are equal. |
5. |
Substitution Property - a value may be substituted for its equal.
|
| 6. |
The whole is equal to the sum of its parts. - also called the Angle Addition Postulate or the Segment Addition Postulate |
| 7. |
Two points determine only one straight line or segment. - postulate used for auxiliary lines |
Of course, there are more properties and postulates that may be used. |
Examples:
|
|
 |
|
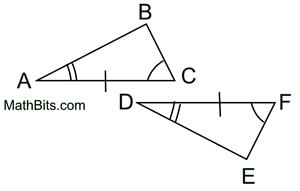
Notice that the given information is marked on the figures. This technique makes it easier to decide which method of proving congruent triangles to use.
(Use ASA for this very simple example.) See Proof. |
|
 |
|
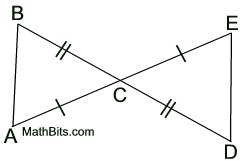
Notice that there seems to be missing information. You are expected to "find" the additional information by observing the vertical angles at C.
(Use SAS for this example.)
See Proof. |
|
 |
|
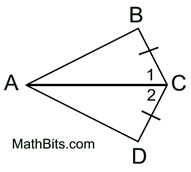
This example contains a "definition". You need to apply the fact that the angle bisector will result in ∠1 being congruent to ∠2. In addition, the two triangles "share" side 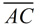 .
(Use SAS for this example.) See Proof. |
|
 |
|
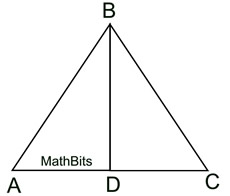
The isosceles definition tells you that 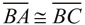 . The altitude definition tells you that 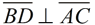 and that ∠ BDC and ∠ BDA are right angles. The triangles share side 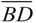 . The sides you need are contained in Δ ABD and
Δ CBD. Use "corresponding parts of congruent Δs are congruent".
(Use HL for the congruent triangles in this example.) See Proof. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|