|
The Addition Rule of Probability is used to find the probability that event A or event B happens.
The final solution will depend upon whether the two events share elements (not mutually exclusive) or do not share elements (mutually exclusive). |
 |
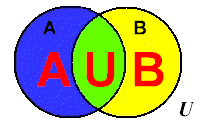
In probability, an outcome is in event "A or B"
when the outcome is in either (or both)
event A and event B.
(Union)
|
|
In a Venn Diagram, an element is in the union of "A or B" only when the element is in set A or set B or BOTH sets. |
"OR" is associated with the concept of union (combining together).
The notation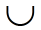 is used for OR (union). is used for OR (union).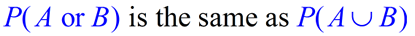
|
Rule (for OR):
(may be referred to as the "Probability Addition Rule")
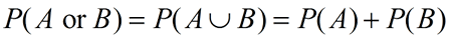
(when A and B are mutually exclusive)
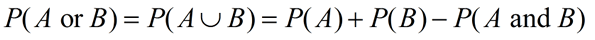
(when A and B are NOT mutually exclusive - elements may overlap)
|
 The rule for "OR" must take into account values that may get counted more than The rule for "OR" must take into account values that may get counted more than
once if elements in the sample spaces should overlap.
Actually, there is really only ONE rule, the second rule.
If sets A and B are mutually exclusive (no elements in common), P(A and B) = 0.
Notice that the two formulas are the same except for the appearance of P(A and B) in the second formula. When P(A and B) = 0, you get the first formula P(A or B) = P(A) + P(B).

A die is rolled. What is the probability that the number is a 4 or the number is a 1? |
Solution:
Sample space = {1, 2, 3, 4, 5, 6}
Event A: Number on the die is a 4; P(A) = 1/6
Event B: Number on the die is a 1; P(B) = 1/6
These outcomes do not overlap. They are mutually exclusive.
From the diagram we can see that there are 2 values that are in A or in B.
Answer: Probability = 2/6 = 1/3
Using the formula: P(A or B) = P(A) + P(B)
= 1/6 + 1/6 = 2/6 = 1/3 |
 Mutually Exclusive
Mutually Exclusive
(They do not overlap.) |

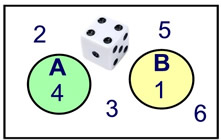
A die is rolled. What is the probability that the number is even or less than 4? |
Solution:
Sample space = {1, 2, 3, 4, 5, 6}
Event A: Numbers on a die that are even: 2, 4, 6; P(A) = 3/6
Event B: Numbers on a die less than 4: 1, 2, 3; P(B) = 3/6
Because of the "overlap", the "2" will be counted twice when the sets are combined. We must subtract one of these occurrences.
From the Venn diagram we can see that there are 5 values that are in A or in B, with the "2" counted only once.
Answer: Probability = 5/6
Using the formula: P(A or B) = P(A) + P(B) - P(A and B)
= 3/6 + 3/6 - 1/6 = 5/6 |
 Not Mutually Exclusive
Not Mutually Exclusive
(They share the element 2.) |

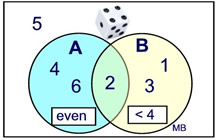
A card is drawn from a deck. What is the probability that the card is red or a face card? |
Solution:
Sample space: 52 cards in the deck
Event A: There are 26 red cards; P(A) = 26/52
Event B: There are 12 face cards total; P(B) = 12/52
There are six cards that are red and a face card (Jack, Queen, and King of hearts and of diamonds). 6 cards could appear twice.
From the diagram we can see that there are 32 values that are in A or in B, with the 6 overlap values counted only once.
Answer: Probability = 32/52 = 8/13
Using the formula: P(A or B) = P(A) + P(B) - P(A and B)
= 26/52 + 12/52 - 6/52 = 32/52 = 8/13 |
 Not Mutually Exclusive.
Not Mutually Exclusive.
They share 6 elements.
|
 |
. |
A die is rolled and a penny is tossed. What is the probability that a head is tossed on the penny or a 3 is rolled on the die? |
Solution:
Sample space (die) = {1, 2, 3, 4, 5, 6}
Event A: Rolling a 3 on a die: P(A) = 1/6
Sample space (penny)= {H, T}
Event B: Tossing a head with the penny: P(B) = 1/2
Probability of OR: These are not mutually exclusive events (but this is not obvious). The 3 can be rolled with both H or T.
Check out the Sample Space for this situation at the right.
Answer: Probability seen from Sample Space = 7/12
Using the formula: P(A or B) = P(A) + P(B) - P(A and B)
= 1/6 + 1/2 - 1/12 = 7/12 |
 
P(A and B) = (H3) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|