|
|
The values that make equations and inequalities TRUE are called "solutions".
|
There are a variety of ways to express solutions to equations and inequalities.
A collection of answers, or solutions, is referred to as a set. The items contained within a set are called elements.
Sets can be described with a variety of notations, such as by roster, by set-builder notation, and by interval notation.
Let's take a look at these notations. |
|
|
 Roster ("Listing") Roster ("Listing") |
A roster is a list of all of the elements in a set, separated by commas, and surrounded by French curly braces. It must be curly braces when denoting a set.
Using a roster to describe a solution may be referred to as expressing the solution in "set notation".
If the set contains "...", it means that the elements continue (in that direction) under the same pattern. ("..." is called an ellipsis.)
A roster can contain any number of elements from no elements to an infinite number. It may be awkward to write a roster for large sets.
The elements in a set are usually listed in increasing order, but may be listed in any order. Elements are not repeated.
|
Examples of rosters:
{ } denotes the empty set. The empty set is also denoted with the symbol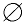 , and sometimes referred to as the null set. , and sometimes referred to as the null set.
{3} is a set with one element, such as the solution to x + 5 = 8.
{-5, 5} is a set with two elements, such as the solution to x2 = 25.
{3, 4, 5, 6 7} is the set of integers from 3 to 7 inclusive.
{... ,-1,0,1 2, 3, ...} means the solution can be any integer value.
|
 Set-Builder Notation Set-Builder Notation |
Set-builder notation is a list of all of the elements in a set, separated by commas, and surrounded by French curly braces.
The symbol " | " is read as "such that". It may also appear as " : ", meaning "such that".
The 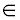 is read "is an element of ". is read "is an element of ".
Set-builder notation is a mathematical shorthand that gives specific details about a set. It may appear in a variety of forms, and may reference different number systems:
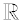 = Real Numbers
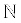 = Natural Numbers {1, 2, 3, 4, ...}
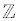 = Integer Numbers {..., -1, 0, 1, 2, 3, ...}
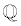 = Rational Numbers (integer top/bottom fractions)
(Read more about number systems.)
|
Examples of set-builder notation:
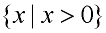 Is read: "the set of all x's, such that, x is greater than 0". Is read: "the set of all x's, such that, x is greater than 0".
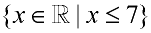 Is read: "the set of x's, x being an element of the Real numbers, such that, x is less than or equal to 7". Is read: "the set of x's, x being an element of the Real numbers, such that, x is less than or equal to 7".
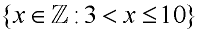 Is read: "the set of x's, x being an element of the Integer numbers, such that, x is greater than 3 and less than or equal to 10". Is read: "the set of x's, x being an element of the Integer numbers, such that, x is greater than 3 and less than or equal to 10".
It is the set {4, 5, 6, 7, 8, 9, 10}.
|
 Interval Notation Interval Notation |
An interval is a connected subset of numbers. Unless told otherwise, assume that "numbers" refers to Real numbers.
Interval notation is a clean and easy way of expressing an interval as an inequality.
In interval notation:
"
( " means "not included" or "open".
" [ " means "included" or "closed".
Infinity is always expressed as being "open".
 The "Open-Interval" form may resemble an "ordered pair" used in graphing. The context of the question will tell you whether (1, 4) means "all numbers between 1 and 4" or "a point that is over 1, up 4 from the origin" on a graph.
Combinations of intervals:
x < 5 or x > 10 becomes (-∞,5) U (10,∞).
The word "or" has been replaced with the symbol"U" which stands for "union", the joining of two sets.
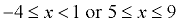
becomes
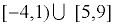 |
Examples of interval notation:
Inequality: 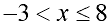
In interval notation: (-3, 8]
Open Interval:
(1, 4)
(a,b) means a < x < b |
|
Closed Interval:
[1, 4]
[a,b] means 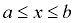 |
|
Half-Open Interval:
(1, 4]
(a,b] means 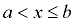 |
|
Half-Open Interval:
[1, 4)
[a,b) means 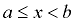 |
|
Non-end Interval:
(1,∞)
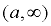 means x > a means x > a |
|
Non-end Interval:
(-∞,4]
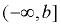 means means 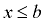 |
|
The notations below all represent the same solution, assuming x is a Real number:
"a number greater than 3
and less than or equal to 9"
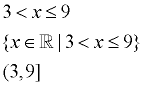
|
If you see 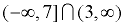 , you are looking for where the two sets overlap. The symbol , you are looking for where the two sets overlap. The symbol 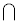 stands for "intersection", which are those points that are in BOTH sets.
This intersection is (3,7]. stands for "intersection", which are those points that are in BOTH sets.
This intersection is (3,7].

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|