|
In algebra, there are some situations that have special patterns of factoring.
Once such situation is factoring the difference of two perfect squares.
This is a pattern (formula) that you will want to remember!
 Factoring the Difference of Two Squares, (a2 - b2) Factoring the Difference of Two Squares, (a2 - b2) |
|
|
We already know that by multiplying: (a + b)(a - b) = a2 - b2.
Remember that the terms (a + b) and (a - b) are called a conjugate pair.
(meaning they are the same expressions but with opposite signs separating the binomial values)
So we know that the product of such conjugate pairs
is the difference (subtraction) of two perfect squares.
If we use the commutative property on the equation above (to reverse the equality), we get:
which now shows the formula for factoring
the difference (subtraction) of two perfect squares, (a2 - b2 ).
Notice that the factors are the conjugate pair, (a + b)(a - b).
By definition, a perfect square is any number that is the square of a rational number,
such as 0, 1, 4, 9, 16, . . . and such as 1/25, 16/81, . . . , etc. |


This formula for factoring does NOT apply to a2 + b2.
It only applies to factoring a2 - b2 . |

Algebraic Perfect Squares
|
In algebra, a term is a perfect square when the numerical coefficient (the number in front of the variable) is a perfect square number, and the exponents of each of the variables are even numbers.
49x2; 25x6; 81y4; 9x2y8; 121x12 are perfect squares.
(A variable is a perfect cube if the exponent is a multiple of three.) |

|
Factor: x2 - 64 |
| |
Solution:
Both x2 and 64 are perfect squares and this problem is subtraction. It qualifies for use of the difference of squares formula. a2 - b2 = (a + b)(a - b)
What times itself will give x2? The answer is x.
What times itself will give 64? The answer is 8.
x2 is the square of x; 64 is the square of 8. a = x and b = 8
[While -x and -8 are also possible, the positive values will make the work easier.]
The factors are (x - 8) and (x + 8)
Answer: x2 - 64 = (x + 8)(x - 8) or (x - 8)(x + 8) |
|
Factor: 9m2 - 81n6 |
| |
Solution:
First, there is a GCF of 9 in these terms. So we can factor out the greatest common factor first: 9(m2 - 9n6 )
In the factor (m2 - 9n6 ), both m2 and 9n6 are perfect squares and this factor is subtraction. It qualifies for use of the difference of squares formula.
a2 - b2 = (a + b)(a - b)
m2 is the square of m; 9n6 is the square of 3n3. a = m and b = 3n3
Answer: 9m2 - 81n6 = 9(m + 3n3 )(m - 3n3 )
(Notice that the GCF of 9 is one of the factors in the answer.) |
 |
Alternate Solution:
If we do not factor out the GCF first, we will get:
Both 9m2 and 81n6 are perfect squares and this problem is subtraction. It qualifies for use of the difference of squares formula. a2 - b2 = (a + b)(a - b)
9m2 is the square of 3m; 81n6 is the square of 9n3. a = 3m and b = 9n3
Almost Answer: 9m2 - 81n6 = (3m + 9n3 )(3m - 9n3 )
While this is a "factored" answer, the answer is not factored completely.
(3 can now be factored from each of the factors)
9m2 - 81n6 = (3m + 9n3 )(3m - 9n3 )
= (3)(m + 3n3 )(3)(m - 3n3 )
Answer: = 9(m + 3n3 )(m - 3n3 ) |
|
Factor: 3x3 - 12x |
Is (a2 - b2)
"hiding" in
this problem? |
Solution:
At first glance, this problem DOES NOT LOOK LIKE a "difference of perfect squares" problem.
BUT, if we factor out the GCF of 3x first, watch what happens.
(3x3 - 12x) = 3x(x2 - 4)
Now, in the factor (x2 - 4), both x2 and 4 are perfect squares and this factor is subtraction. It now qualifies for use of the difference of squares formula.
a2 - b2 = (a + b)(a - b)
x2 is the square of x; 4 is the square of 2. a = x and b = 2
Answer: 3x3 - 12x = 3x(x + 2)(x - 2)
(Don't forget to bring along GCF of 3x as one of the factors in the answer.)
|

|
Factor: x2 - 9 using Algebra Tiles |
KEY: 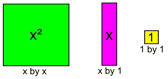 See more about Algebra Tiles.
Remember that the "red" tiles represent negative values.
See more about Algebra Tiles.
Remember that the "red" tiles represent negative values.
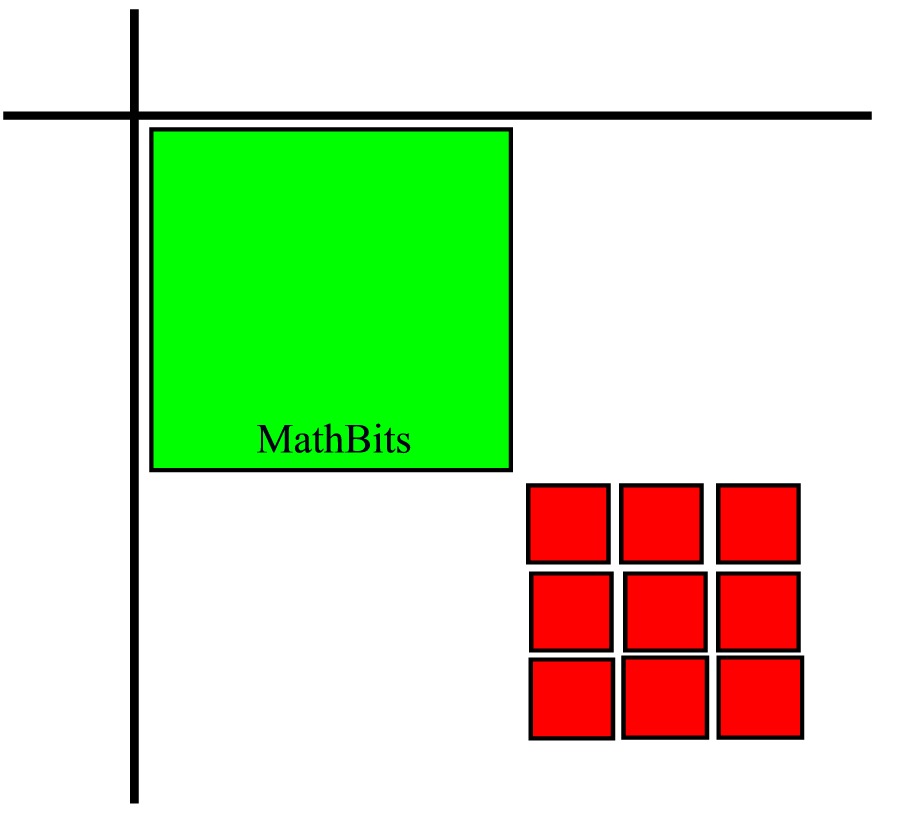
Place the x2 tile and the -9 (red)
tiles in the grid.
|
Fill in the empty spaces with x-tiles that do not change the value of the current entries.
(1 x-tile + 1 red x-tile = 0). 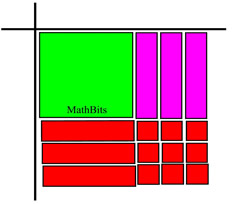 |
Fill the outside sections of the grid with x-tiles and 1-tiles that complete the pattern.
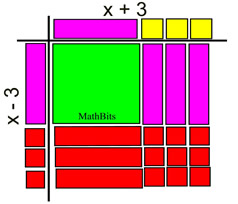 |
Filling in the missing tiles shows that the factors will be (x - 3) and (x + 3).
x2 - 9 = (x - 3)(x+3)
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|








